Quando vamos abordar um cálculo de probabilidade, partimos do conceito de Fatoriais.
O cálculo fatorial nos permite saber quais são as combinações possiveis de uma determinada quantidade de elementos através da seguinte fórmula:
O cálculo fatorial nos permite saber quais são as combinações possiveis de uma determinada quantidade de elementos através da seguinte fórmula:
Por exemplo, número de combinações possíveis feita por 5 elementos é de 120, partindo do conceito de 5 fatorial (5!):
(Fatorial: Multiplique o número fatorial por todos os demais números que o antecedem até o 1, para encontrar seu valor.)
Utilizando, por base o exemplo exposto pelo fisico Adauto J. B. Lourenço (Lourenço, A.J.B. Como tudo começou. Editora Fiel. Pg 32): Se calculássemos as possíveis combinações quando utilizamos estas 4 letras: G A T O.4! (4! = 4x3x2x1 = 24) teríamos 24 possibilidades:
TGAO GTAO AOTG OTGA
TGOA GTOA AOGT OTAG
TAOG GOTA AGOT OATG
TAGO GOAT AGTO OAGT
TOAG GATO ATGO OGTA
TOGA GAOT ATOG OGAT
Nem todas as palavras produzidas possuem significado. Considereando que, na lingua portuguesa, apenas 3 palavras em 24 fazem sentido, a probabilidade é de 1 para 8.
Um única letra fora do lugar não permite que a palavra de forme, dessa forma a ordem das letras se torna um elemento fundamental.
No exemplo do bolo de chocolate produzido aleatoriamente no caminhão que capotou, teríamos que levar em consideração não somente a quantidade que teria caído dentro do cantil, mas também a probabilidade daquela quantidade cair dentro da metade do cantil.
É muito importante que exista uma alta probabilidade para um evento acontecer, conforme o proposto por uma teoria. A própria ciência tem limites traçados para dizer quando é possivel que algo aconteça. Na linguagem da matemática, algo que jamais aconteceria ou teria acontecido tem uma probabilidade que se aproxima de zero.
Segundo Carl Sagan, Francis Crick e L.M. Muchin a probabilidade do homem ter evoluído é de 1 em 10²ººººººººº. Emile Berel demonstrou que eventos com probabilidade de 1 entre 150 simplesmente não ocorrem.
(Carl Sagan, F. H. C. Crick, L M. Muchin, Communication and Extraterrestrial Intelligence , Ed Cambrigde, MA, pg 45-46)
(Emile Borel, Probabilities and Life, New York, Dover, cp 1-3)
Utilizando, por base o exemplo exposto pelo fisico Adauto J. B. Lourenço (Lourenço, A.J.B. Como tudo começou. Editora Fiel. Pg 32): Se calculássemos as possíveis combinações quando utilizamos estas 4 letras: G A T O.4! (4! = 4x3x2x1 = 24) teríamos 24 possibilidades:
TGAO GTAO AOTG OTGA
TGOA GTOA AOGT OTAG
TAOG GOTA AGOT OATG
TAGO GOAT AGTO OAGT
TOAG GATO ATGO OGTA
TOGA GAOT ATOG OGAT
Nem todas as palavras produzidas possuem significado. Considereando que, na lingua portuguesa, apenas 3 palavras em 24 fazem sentido, a probabilidade é de 1 para 8.
Um única letra fora do lugar não permite que a palavra de forme, dessa forma a ordem das letras se torna um elemento fundamental.
No exemplo do bolo de chocolate produzido aleatoriamente no caminhão que capotou, teríamos que levar em consideração não somente a quantidade que teria caído dentro do cantil, mas também a probabilidade daquela quantidade cair dentro da metade do cantil.
É muito importante que exista uma alta probabilidade para um evento acontecer, conforme o proposto por uma teoria. A própria ciência tem limites traçados para dizer quando é possivel que algo aconteça. Na linguagem da matemática, algo que jamais aconteceria ou teria acontecido tem uma probabilidade que se aproxima de zero.
Segundo Carl Sagan, Francis Crick e L.M. Muchin a probabilidade do homem ter evoluído é de 1 em 10²ººººººººº. Emile Berel demonstrou que eventos com probabilidade de 1 entre 150 simplesmente não ocorrem.
(Carl Sagan, F. H. C. Crick, L M. Muchin, Communication and Extraterrestrial Intelligence , Ed Cambrigde, MA, pg 45-46)
(Emile Borel, Probabilities and Life, New York, Dover, cp 1-3)

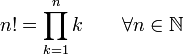
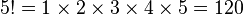









Nenhum comentário:
Postar um comentário